Probability density function
Page 1 of 1
 Probability density function
Probability density function
The length of time, in minutes, that a customer queues in a Post Office is a random variable, T, with probability density function
=\left\{\begin{matrix}&space;c(81-t^2)&space;&&space;0\leqslant&space;t\leqslant&space;9\\&space;0&&space;\text{otherwise}&space;\end{matrix}\right.)
where c is a constant
(a) Show that the value of c is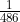
(b) Show that the cumulative distribution function F(t) is given by
=\left\{\begin{matrix}&space;0&space;&&space;t<&space;0\\&space;\frac{t}{6}&space;-\frac{t^3}{1458}&&space;0\leqslant&space;t\leqslant&space;9\\&space;1&&space;t>&space;9&space;\end{matrix}\right.)
(c) Find the probability that a customer will queue for longer than 3 minutes.
A customer has been queueing for 3 minutes.
(d) Find the probability that this customer will be queueing for at least 7 minutes.
Three customers are selected at random.
(e) Find the probability that exactly 2 of them had to queue for longer than 3 minutes.
where c is a constant
(a) Show that the value of c is
(b) Show that the cumulative distribution function F(t) is given by
(c) Find the probability that a customer will queue for longer than 3 minutes.
A customer has been queueing for 3 minutes.
(d) Find the probability that this customer will be queueing for at least 7 minutes.
Three customers are selected at random.
(e) Find the probability that exactly 2 of them had to queue for longer than 3 minutes.
Page 1 of 1
Permissions in this forum:
You cannot reply to topics in this forum|
|
|
